Несущие крылья. Часть 1. Профиль крыла.
"Человек не имеет крыльев и по отношению веса своего
тела к весу мускулов он в 72 раза слабее птицы….
Но я думаю, что он полетит, опираясь не на силу
своих мускулов, а на силу своего разума."
Н.Е. Жуковский
Моделизмом можно заниматься по-разному. Для людей амбициозных это спорт, соревнования и утверждение своего «Я» среди коллег. Для остальных это просто хобби. Кто-то больше любит летать, кто-то строить самолеты. Есть еще категория людей творческих, стремящихся не просто ходить по проторенным дорожкам, но и пробовать, а что там, рядом, может более интересно? Это категория конструктора-любителя. От профессионала он отличается чаще всего отсутствием специального образования. Читать учебники по аэродинамике для «Большой» авиации дело непростое. А привнести в модель что-то свое хочется. Экспериментировать же наобум – малопродуктивное занятие. Из этого тупика часто раздаются возгласы: дескать, нечего тут придумывать, все уже придумано до нас; бери Экстру и делай по готовым чертежам. Или: нету тут никаких теорий, в моделях все – эмпирика! Не соглашаясь ни с теми, ни с другими. Предлагаем вниманию людей творческих введение в теорию несущего крыла. Для простоты восприятия, здесь почти нет формул и количественных соотношений. Все зависимости даются качественно, по принципу: данный параметр влияет на то-то в ту сторону. Это полезно знать не только конструкторам, но и пилотам, интересующимся, почему модель в воздухе ведет себя так, а не иначе. Заодно введем элементарную терминологию, чтобы моделист не измерял крыло в «длину» и «ширину». Часть первая посвящена только профилю крыла. Во второй части будут рассмотрены все остальные аспекты аэродинамики крыла.
Терминология
Чтобы однозначно понимать друг–друга при рассуждениях, рассмотрим основные понятия геометрии профиля крыла. Поперечное сечение крыла плоскостью, параллельной плоскости его симметрии называется « профилем». Типовой профиль крыла выглядит так:
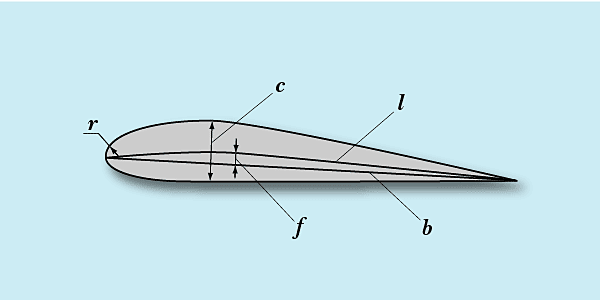
Максимальное расстояние между крайними точками профиля – b , называется хордой профиля. Наибольшая высота профиля – c , называется толщиной профиля, а ее расстояние от передней точки – координатой максимальной толщины. Линию, точки которой равноудалены от верхней и нижней образующих профиля - l, называют средней линией профиля. Ее максимальное расстояние от хорды – f, называется кривизной профиля, а удаление от передней точки – координатой максимальной кривизны. Носик профиля образован некоей кривой линией, минимальный радиус которой обозначают – r, это радиус скругления носика профиля. Поскольку качественно надо сравнивать разные профили разных размеров, договорились все указанные величины измерять относительно хорды профиля. Зачастую при этом даже опускают слово «относительная». Просто, если толщина профиля указана в %, то всем ясно, что это отношение реальной толщины к величине хорды профиля. На данном рисунке верхняя линия, образующая профиль одной формы, а нижняя – другой. Такой профиль называется несимметричным. Если же, одна образующая, является зеркальным отражением другой, то профиль называется симметричным. Нетрудно сообразить, что кривизна симметричного профиля равна нулю.
Картина обтекания профиля
Всем известно, что крыло создает подъемную силу, только тогда, когда оно движется относительно воздуха. Т.е. характер обтекания воздухом верхней и нижней поверхностей крыла непосредственно создает подъемную силу. Как это происходит?
Рассмотрим профиль крыла в потоке воздуха:
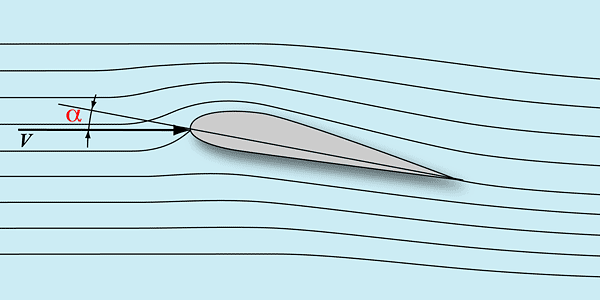
Здесь линии течения элементарных струек воздуха обозначены тонкими линиями. Профиль к линиям течения находится под углом атаки а – это угол между хордой профиля и невозмущенными линиями течения. Там, где линии течения сближаются, скорость потока возрастает, а абсолютное давление падает. И наоборот, где они становятся реже, скорость течения уменьшается, а давление возрастает. Отсюда получается, что в разных точках профиля воздух давит на крыло с разной силой. Разницу между местным давлением у поверхности профиля и давлением воздуха в невозмущенном потоке можно представить в виде стрелочек, перпендикулярных контуру профиля, так что направление и длина стрелочек пропорциональна этой разнице. Тогда картина распределения давления по профилю будет выглядеть так:
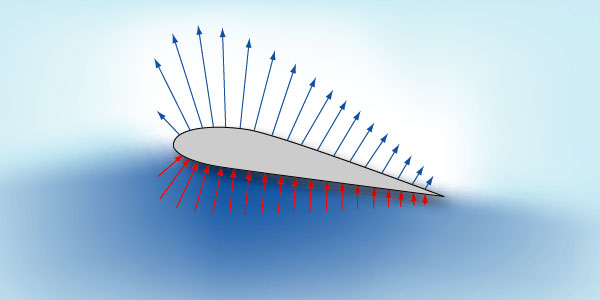
Здесь хорошо видно, что на нижней образующей профиля имеется избыточное давление – подпор воздуха. На верхней же, - наоборот, разряжение. Причем оно больше там, где выше скорость обтекания. Примечательно здесь то, что величина разряжения на верхней поверхности в несколько раз превышает подпор на нижней. Векторная сумма всех этих стрелочек и создает аэродинамическую силу R, с которой воздух действует на движущееся крыло:
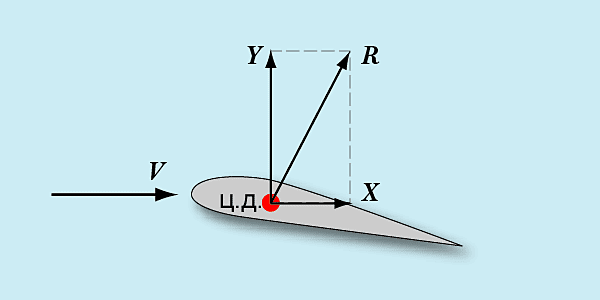
Разложив эту силу на вертикальную Yи горизонтальную X компоненты, мы получим подъемную силу крыла и силу его лобового сопротивления. Из картины распределения давления видно, что львиная доля подъемной силы образуется не из подпора на нижней образующей профиля, а из разряжения на верхней, что опровергает весьма распространенное заблуждение начинающих моделистов.
Точка приложения силы R зависит от характера распределения давления по поверхности профиля. При изменении угла атаки, распределение давления тоже будет изменяться. Вместе с ним будет меняться и векторная сумма всех сил по абсолютной величине, направлению и точке приложения. Кстати, последнюю называют центром давления. С ним тесно связано понятие фокуса профиля. У симметричных профилей эти точки совпадают. У несимметричных положение центра давления на хорде при изменении угла атаки меняется, что очень затрудняет расчеты. Чтобы их упростить, было введено понятие фокуса. При этом равнодействующую аэродинамических сил разделили не на две компоненты, а на три – к подъемной силе и силе лобового сопротивления добавился еще момент крыла. Такой, вроде бы нелогичный прием позволил, поместив точку приложения подъемной силы в фокусе профиля, зафиксировать его положение и сделать его независящим от угла атаки. Прием удобный, только не надо забывать о появившемся при этом моменте крыла.
Разряжение на верхней части профиля можно не только измерить приборами, но и при определенных условиях увидеть собственными глазами. Как известно, при резком расширении воздуха, содержащаяся в нем влага может мгновенно конденсироваться в капельки воды. Кто бывал на авиашоу, мог видеть, как во время резкого маневрирования самолета, с верхней поверхности крыла срываются струйки белой пелены. Это и есть водяной пар, сконденсировавшийся при разряжении в мелкие капельки воды, которые очень быстро снова испаряются и становятся невидимыми.
Размер имеет значение!
Зависит ли характер обтекания от размеров профиля и фактической скорости движения крыла относительно воздуха? Да, и очень сильно. Связано это с физическими свойствами воздуха, главными из которых являются упругость, плотность и вязкость.
Упругость (еще говорят, сжимаемость) важна только при скоростях движения, сопоставимых со скоростью звука. В моделизме такие скорости встречаются лишь на концах лопастей воздушного винта. Поскольку мы занимаемся сейчас крылом, про это свойство воздуха можем забыть.
Массовая плотность воздуха является главной причиной возникновения подъемной силы крыла. Уже на втором рисунке видно, что направления линий обтекания воздуха до крыла и после него несколько не совпадают. Т.е. крыло скашивает поток воздуха вниз. Поскольку поток обладает определенной массой, то по закону сохранения импульса на крыло действует сила R. Отсюда следует простая зависимость, чем воздух плотнее, тем при прочих равных условиях больше подъемная сила. На большой высоте плотность воздуха снижается, но для моделей это не важно, - они так высоко не летают. А вот увеличение плотности воздуха при снижении его температуры заметно уже для моделей. Один и тот же самолет зимой сможет выполнить петлю меньшего радиуса, чем летом.
Вязкость воздуха, - словосочетание непривычное. Вязкость автомобильного масла – это понятно, а воздуха? Тем не менее, воздух тоже обладает определенной вязкостью. Причем причины и механизм ее возникновения такие же, как и у автомобильного масла, только величина намного меньше. Слои воздуха движутся друг относительно друга с трением. Очень маленьким, но не нулевым. В картине обтекания крыла вязкость приводит к тому, что у самой поверхности профиля на границе между твердой поверхностью и потоком воздуха возникает тоненький слой воздуха, как бы присоединенный к крылу и движущийся вместе с крылом. Его так и называют – пограничный слой. Поведение этого слоя сильно зависит от размеров профиля и скорости его обтекания воздухом. Для того чтобы оценивать степень влияния вязкости воздуха на характер обтекания крыла при разных условиях придумали коэффициент, равный произведению хорды крыла (в метрах) на скорость его движения относительно воздуха (в метрах в секунду), деленному на вязкость воздуха. Называется этот коэффициент числом Рейнольдса в честь английского физика и обозначается так: Re. В моделистских применениях вязкость воздуха можно считать постоянной без большой погрешности и равной 0,000015 м 2/сек. Будет удобнее считать число Рейнольдса по приближенной формуле Re=70*V*b. Здесь скорость надо подставить в метрах в секунду, а хорду в миллиметрах. Чтобы было понятнее, приведем пример. Крыло модели планера с хордой 0,1 метр летит со скоростью 6 метров в секунду. Получаем Re=42000. Это очень маленькое значение для летающих моделей и характерно для свободнолетающих моделей класса F1. При таких значениях Re вязкость имеет огромное значение. Обтекание профиля при этом выглядит так:
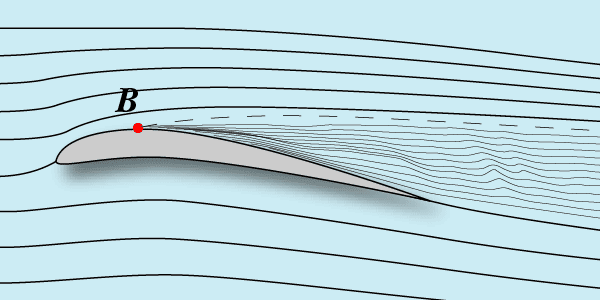
Здесь интересно обратить внимание на точку В. До нее течение воздуха в пограничном слое плавное, без перемешивания прислойных струек. Такое течение называется ламинарным. В нем практически нет маленьких воздушных вихрей, перемешивающих воздух из соседних слоев. В точке В начинается образование прислойных вихрей, перемешивающих воздух из соседних слоев. Такое течение называется турбулентным. Можно так построить форму образующей профиля, что на его большей верхней части течение воздуха будет ламинарным, а точка В сдвинется назад по профилю. Такие профили называют ламинаризованными. Какое течение лучше для модели? Здесь однозначного ответа на все случаи жизни нет. Ламинарное течение в сравнении с турбулентным имеет свои преимущества и недостатки. Здесь назовем только достоинство – при ламинарном течении трение поверхности крыла о воздух меньше. Значит и меньше лобовое сопротивление. О недостатках ламинарного обтекания поговорим позже.
Для модели пилотажки с хордой крыла 0,3 метра и скоростью 20 метров в секунду получается Re=400000. Обтекание профиля будет выглядеть так:
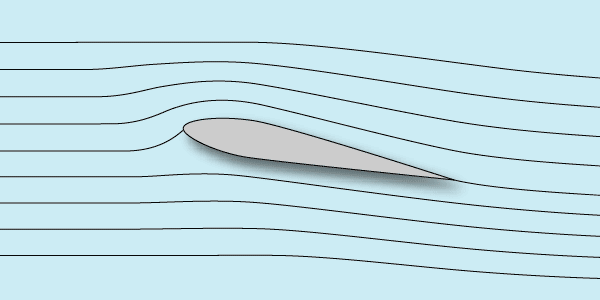
Очень похоже? Да, но профиль не тот. А что будет, если планерный профиль разогнать до этих скоростей? Или наоборот, пилотажный профиль поставить на планер F1? Это мы рассмотрим также попозже. А сейчас посмотрим, как посчитать подъемную силу и лобовое сопротивление крыла.
Скоко точно в граммах?
Совсем обойтись без формул не получится. Да и не интересно это. Приведем лишь две.
Подъемная сила крыла:
Y= Cy* p*V 2*S/2
Сила лобового сопротивления:
X= Cx* p*V 2*S/2
Здесь:
p - массовая плотность воздуха
V - скорость движения крыла относительно воздуха
S - площадь крыла
Cy - коэффициент подъемной силы крыла (читается – це игрек)
Cx – коэффициент лобового сопротивления крыла (читается – це икс)
Совершенно понятно, что вся «собака зарыта» в этих коэффициентах подъемной силы и лобового сопротивления. Оба они сильно зависят от угла атаки крыла, но по-разному. Для типичного несимметричного профиля зависимости эти выглядят так:
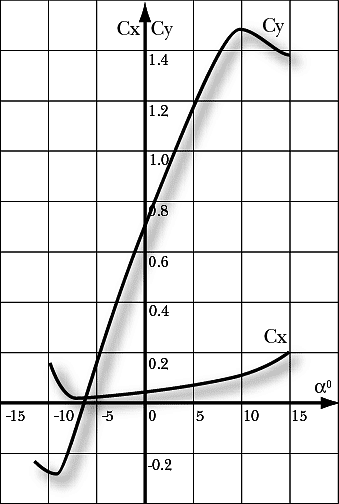
Здесь много интересного. Попробуем разобраться, почему графики идут так, а не иначе. Начнем с нулевого угла атаки. Как видно из графика при нем подъемная сила не равна нулю. Это связано с разными верхней и нижней образующими профиля, т.е. с ненулевой его кривизной. Верхняя образующая более выпуклая, чем нижняя поэтому давление распределяется так:
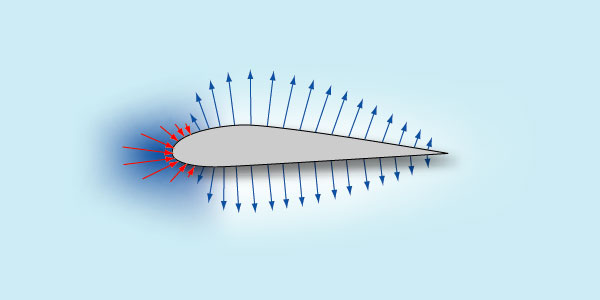
Чтобы подъемная сила несимметричного профиля стала бы равной нулю, его надо расположить под отрицательным углом атаки.
По мере увеличения угла атаки, коэффициент подъемной силы растет почти пропорционально. При этом подпор на нижней образующей профиля растет не сильно, а разряжение на верхней образующей растет в разы. Если внимательно посмотреть на распределение давления по верху профиля, можно заметить большой перепад давления с задней половины профиля на переднюю, то есть перепад направлен навстречу потоку обтекания. Пока он не слишком велик, скоростной напор обтекающего воздуха справляется с ним. Но, начиная с некоторого угла атаки, этот перепад становится причиной возникновения обратного тока воздуха вдоль второй половины верхней образующей профиля:
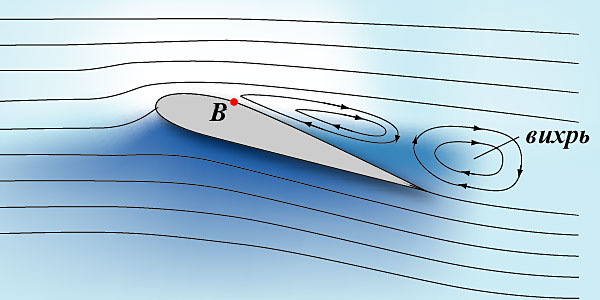
В точке В происходит отрыв пограничного слоя от поверхности крыла. За точкой отрыва возникает вихревое обтекание с линиями обратного тока. Происходит срыв потока. При дальнейшем небольшом увеличении угла атаки Су вначале слегка возрастает. Но точка отрыва быстро перемещается вперед по верхней образующей, после чего Су начинает падать. Угол атаки, на котором достигается перегиб кривой Су, называется критическим углом атаки.
Теперь обратимся к Сх. При нулевой подъемной силе он минимален. Лобовое сопротивление при этом обусловлено двумя компонентами: трением воздуха о поверхность крыла и динамическим сопротивлением, смысл появления которого хорошо виден на рисунке 8. Видите там стрелочки, направленные на носик профиля. Лобовое сопротивление, состоящее из этих двух компонент, называют профильным сопротивлением. По мере увеличения угла атаки появляется и растет подъемная сила крыла. Лобовое сопротивление при этом тоже растет, сначала медленно, потом быстрее. Разницу между лобовым сопротивлением при ненулевой подъемной силе и профильным сопротивлением называют индуктивным сопротивлением. Оно в широких пределах пропорционально квадрату Су. При срыве обтекания Сх быстро растет и не убывает при дальнейшем росте угла атаки.
Обратите внимание, как изменяется Су в диапазоне отрицательных углов атаки. Линейный рост довольно быстро заканчивается, а критический угол атаки наступает гораздо раньше, чем при положительных углах и при намного меньшем абсолютном значении Су. Отсюда становится понятным, почему при несимметричном профиле крыла прямая и обратная петли самолета, столь сильно отличаются по величине минимального радиуса. Для симметричного профиля линия Су для отрицательных углов повторяет зеркально линию для положительных углов. Поэтому на пилотажных самолетах применяют чаще всего симметричные профили.
Качество профиля, поляра
Аэродинамическим качеством профиля называется отношение подъемной силы к лобовому сопротивлению. Сам термин качество происходит из функции крыла – оно призвано создавать подъемную силу. А то, что при этом появляется побочный эффект – лобовое сопротивление, явление вредное. Поэтому логично отношение пользы к вреду назвать качеством. Если построить зависимость Су от Сх на графике:
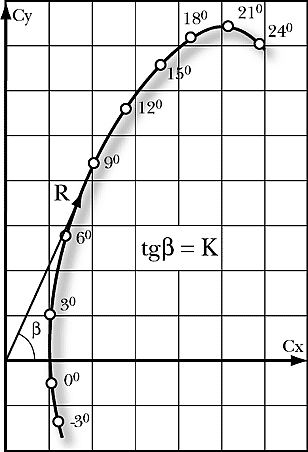
то эту линию называют полярой профиля. Полярой она называется не случайно. Кто помнит из школы, что кроме привычных прямоугольных координат, еще бывают полярные, тот быстро поймет, что эта же кривая в полярных координатах дает зависимость длины отрезка между началом координат и любой точкой на поляре от угла наклона этого отрезка к горизонтальной оси. Так вот, длина отрезка пропорциональна полной аэродинамической силе R, действующей на крыло, а тангенс упомянутого угла равен аэродинамическому качеству К. Т.е. поляра позволяет очень просто оценивать изменение аэродинамического качества профиля крыла. Для удобства, на кривую принято наносить реперные точки, отмечающие соответствующий угол атаки крыла. По поляре легко оценить профильное сопротивление, максимально достижимое аэродинамическое качество профиля и его другие, важные параметры. Поляра зависит от числа Re. Свойства профиля удобно оценивать по семейству поляр, построенных в одной сетке координат для различных чисел Re.
Поляры конкретных профилей получают двумя способами:
- Продувками в аэродинамической трубе
- Теоретическими расчетами.
Следует заметить, что в последнее время теория, вкупе с компьютерными достижениями, позволила создать программы рассчитывающие поляры, довольно точно совпадающие с экспериментальными продувками. Например, весьма удобной для любительских целей программой для построения поляр с большой базой данных по геометрии известных профилей, является программа Profili, разработанная итальянскими моделистами. В этой программе Су обозначается как Cl, а Сх - как Cd.
Поляра, это один из самых наглядных способов оценки свойств профиля для конкретных применений. По этой кривой легко оценить изменение подъемной силы и лобового сопротивления при изменении угла атаки и их соотношение, то есть качество. По семейству поляр для разных чисел Re просто оценивается поведение этих сил при изменении скорости. Характер кривой в диапазоне малых подъемных сил в диапазоне скоростей показывает способность крыла разгоняться в пикировании самолета. Кривая на больших Су показывает способность к парению на малых скоростях, а ее плавный или резкий изгиб, характеризует темп сваливания при срыве потока обтекания. Асимметрия и поведение поляры в районе отрицательных Су показывает способность крыла к перевернутому полету, обратным петлям и демонстрирует, насколько они будут отличаться от прямого полета и прямых фигур. По семействам поляр нескольких профилей удобно проводить сравнительный анализ их свойств и выбирать наиболее подходящий для конкретного применения.
Для малых скоростей
Познакомившись с основными понятиями, рассмотрим особенности аэродинамики профиля крыла при разных расчетных значениях Re.
Самыми тихоходными летающими моделями являются комнатные модели класса F1D. Скорости полета у них настолько малы, что их аэродинамика вообще не изучена. Кроме этого класса такие числа нигде больше не используются. Профиля крыла там, собственно и нет. Точнее он вырождается в тончайшую, толщиной в несколько микрон изогнутую пленку. Далее мы о таких моделях говорить не будем, – слишком уж они специфичны.
Следующими тихоходами являются свободнолетающие модели класса F1. Как известно, для этих моделей главной задачей является максимум времени парения в воздухе. Поскольку правилами ограничена минимальная нагрузка на крыло (отношение веса модели к площади его крыла), то увеличение продолжительности полета достигается за счет максимально возможного значения Су. При этом аэродинамическое качество получается отнюдь не наибольшим, но оно и не важно. Даже внутри класса F1 используются разные профили, попробуем разобраться - почему?
На свободнолетающих планерах – класс F1A используются профили с очень большой кривизной. Они позволяют летать на минимально-возможной скорости с очень большим значением Су. Часто используются профили Бенедека, слегка модифицированные. Сейчас у национальных спортсменов популярен профиль Макарова-Кочкарева – именитых московских спортсменов:
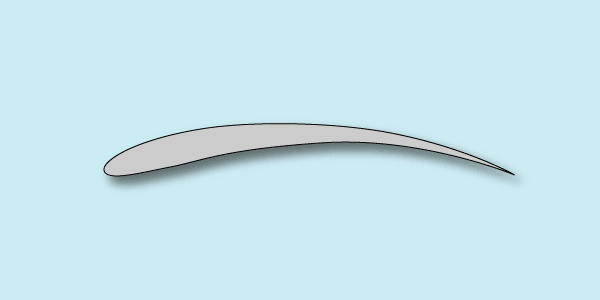
У таких профилей есть она особенность – работа на низких значениях Re. В этом случае скоростной напор невелик, и допустимый перепад давлений вдоль верхней дуги профиля – тоже. Работа на углах атаки, близких к критическому, создает угрозу к срыву обтекания и проваливанию модели. Для оптимизации обтекания применяют специальные меры. В частности, для увеличения толщины пограничного слоя (толстый пограничный слой более устойчив) используют для обтяжки крыла материал с повышенной шероховатостью. У более шероховатой поверхности силы трения о воздух больше, чем у гладкой. Это, конечно, снижает аэродинамическое качество, но позволяет использовать большие углы атаки и большее Су, что важно для увеличения продолжительности полета. Сейчас используется специальная двухслойная пленка с шероховатой поверхностью. В прошлом – микалентные длинноволокнистые сорта бумаги.
Выше уже говорилось о двух режимах обтекания – ламинарном и турбулентном. Достоинством ламинарного обтекания профиля является малое трение крыла о воздух, и как следствие – меньшее его профильное сопротивление. Но ламинарное течение в пограничном слое снижает его устойчивость к отрыву от профиля при увеличении угла атаки. Турбулентный пограничный слой отрывается позже ламинарного, при больших углах атаки и больших Су. Чтобы поднять несущие свойства профиля на крыльях планеров F1A устанавливают специальный турбулизатор, который создает в пограничном слое вихри и повышает его устойчивость к отрыву. Чаще всего турбулизатор представляет из себя тонкую нить, приклеенную в нескольких миллиметрах от носика профиля на верхней поверхности крыла. Чтобы он не провоцировал преждевременный срыв потока, иногда его приклеивают зигзагообразно. Профиль планеров F1A оптимизирован только под один режим полета – парение, поскольку во время затяжки леером его аэродинамические свойства играют второстепенную роль.
У резиномоторных моделей класса F1B помимо парения есть еще режим моторного полета. Поскольку скорость моторного полета невелика, на этих моделях часто используют те же профили что и на F1A. Некоторые моделисты используют профили с меньшей кривизной. Дело в том, что большое значение кривизны профиля обуславливает и значительное профильное сопротивление крыла. На моторном режиме нет потребности в высоком значении Су, и повышенное профильное сопротивление на малых углах атаки снижает скорость набора высоты.
Некоторые спортсмены в этом классе успешно используют управление пограничным слоем. Для этого в верхней обшивке крыла делаются два ряда отверстий – в районе максимального разряжения и недалеко от задней кромки крыла, где разряжение невелико:
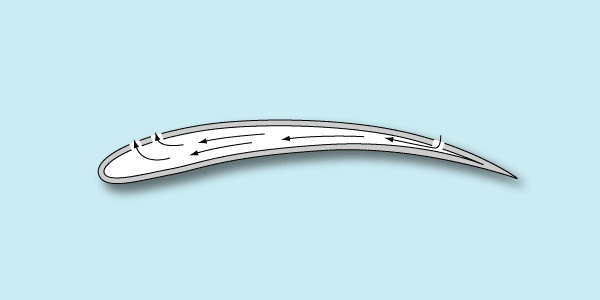
За счет разности давлений часть воздуха через второй ряд отверстий отсасывается и подается внутри полости крыла на передний ряд, - в зону максимального разряжения. Подача дополнительного воздуха в эту зону оттягивает срыв потока на большие углы атаки, за счет чего достигается большее значение Су. Попутно отметим, что сдув и отсос пограничного слоя широко используется на больших самолетах (истребителях) при взлетно-посадочных режимах. Там, правда, совсем другие числа Re.
Особенно значима двухрежимность работы крыла на таймерных моделях класса F1C. Здесь время моторного полета жестко ограничено пятью секундами, и при равной мощности мотора, высота взлета определяется Сх крыла. Если на таймерку поставить профиль с F1A, то высота взлета уменьшится, что не компенсируется более высоким Су на этапе парения. Поэтому профиль для таймерных моделей выбирается как компромисс между малым значением Сх при нулевой подъемной силе (таймерки взлетают вертикально) и высоким значением Су.
Представляет интерес техническое решение, которое можно смело назвать бескомпромиссным. Чемпион России и Европы в классе F1C Леонид Фузеев из Саратова сделал крыло таймерки складным втрое. На этапе моторного взлета консоли крыла складываются, образуя симметричный профиль крыла в 2,5 раза меньшего размаха:
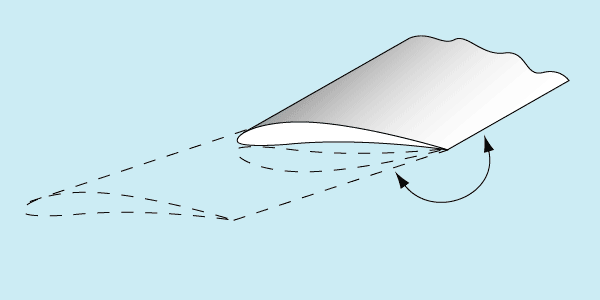
После набора высоты и остановки мотора крыло раскладывается в полный размах. По наблюдениям автора на финале последнего Чемпионата России, модель Фузеева взлетает не выше других призеров. Сказывается высокая толщина профиля сложенного крыла. Однако, на этапе парения она не оставляет надежд другим моделям, поскольку Леонид применил чисто планерный профиль Макарова-Кочкарева с большой кривизной.
Так подробно рассмотрены профили свободнолетающих моделей потому, что многолетняя история развития сформировала их весьма высокое техническое совершенство. У моделистов периодически возникает соблазн заимствовать готовые решения из класса F1 для радиоуправляемых моделей. С одним из таких решений – классическим чемпионатным планером F1A, конвертированным в радиоуправляемый для выступления в классе кроссовых планеров, автор познакомился на прошлогодних межнациональных соревнованиях самолетостроительных предприятий в Орле МАП-2003. Такую конструкцию привез молодой спортсмен из Запорожья. С точки зрения развлекательной – это интересное решение. Однако, по летным качествам для спортивных целей оно интереса не представляет. Профиль с большой кривизной хорош только для полетов модели вместе с потоком воздуха на минимальных относительных скоростях. Попытка рулить таким планером против даже слабого ветра, показала его непригодность для управляемого полета, - планер либо сносило ветром, либо он просто сыпался с высоты.
Для высоких скоростей
Летательные аппараты этой группы оптимизированы под однорежимный полет с максимальной скоростью. Из спортивных классов сюда можно отнести кордовых скоростников F2A и гоночные группы D, кордовые F2C, радио-ДВСки F3D и радио-электрички F5D. А также многочисленные экспериментальные и рекордные самолеты. Поскольку скорость полета этих самолетов очень высокая, то характер поведения Су мало кого волнует. Скоростной напор очень высок и полет проходит при малых углах атаки и малых значениях Су. Главное для профиля этих моделей, - минимально возможное значение Сх при крейсерской скорости полета. Его значение зачастую определяет лобовое сопротивление всего самолета. Такая оптимизация достигается уменьшением толщины профиля до величин, когда определяющим становится уже не аэродинамика обтекания, а строительная прочность и жесткость крыла на кручение. Применение современных высокопрочных и высокомодульных композитных материалов позволило уменьшить толщину профиля гоночных моделей до 5 – 7 %. Кривизна профиля применяется около 1 – 2% для возможности крейсерского полета с нулевым углом атаки, Сх – при этом минимален. Вместе с острым носиком типовой гоночный профиль выглядит так:
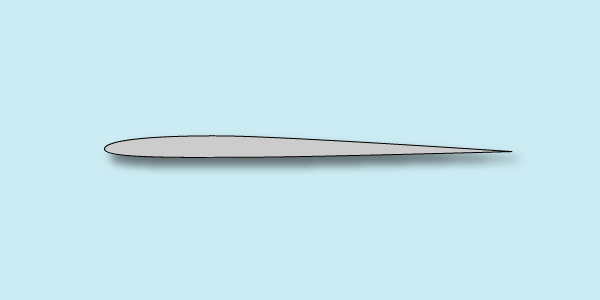
Такие профили плохо работают на взлетно-посадочных режимах, когда скорость полета невелика. Самолет с таким профилем имеет плохие штопорные характеристики и маленький критический угол атаки. Острый носик и почти плоская верхняя поверхность профиля легко провоцируют срыв обтекания. Поэтому сажать такие самолеты приходится на больших скоростях, что требует высокого мастерства пилота. Типовое значение чисел Re для этой группы профилей может легко превысить 1000000.
Пилотажный самолет
Для пилотажного самолета, наряду с другими требованиями, важна симметрия летных характеристик для прямого и перевернутого полета. Поэтому в их крыльях используются исключительно симметричные профили. Относительная толщина профиля, определяется исходя из предполагаемых чисел Re при выполнении фигур. Для классического пилотажа типовая толщина профиля – 12-15 %. Чтобы обеспечить качественное исполнение срывных фигур, таких как «штопор» и «штопорная бочка» носик профиля имеет достаточно малый радиус скругления.
Фан-флаи тоже предназначены для выполнения пилотажных фигур, но на гораздо меньших скоростях. Для них важен плавный, а не резкий срывной режим. Толщина профиля здесь до 20% и максимально большой радиус скругления носика профиля. Почему радиус скругления так влияет на срывные характеристики? Обратимся к картине обтекания толстого профиля с тупым носиком на малом и большом углах атаки
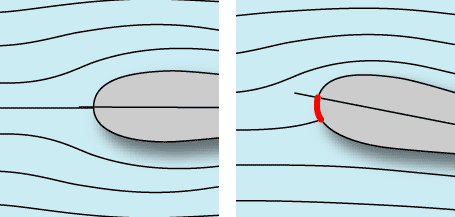
Хорошо видно, что точка разделения верхнего и нижнего пограничных слоев при изменении угла атаки перемещается по образующей носика. Поэтому переход к срыву потока при увеличении угла атаки здесь происходит позже и более плавно.
Для острого носика такое перемещение приводит к локальному резкому повышению скорости обтекания в месте большой крутизны носика. Такое повышение провоцирует более ранний отрыв пограничного слоя сразу от носика профиля. На графиках Cy=f(a) это выражается так:
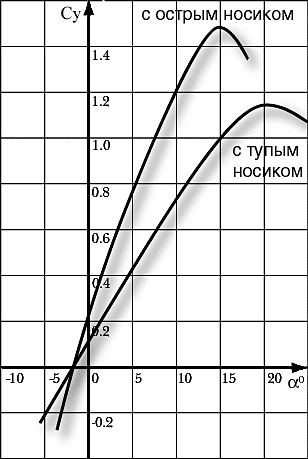
Частный случай пилотажки – учебно-тренировочный самолет. Вообще то сочетание этих названий в одном самолете не совсем правильное. Для учебного самолета хорошо подходит плоско-выпуклый профиль ClarkY, с относительной толщиной 15-18%. Он обеспечивает при прочих равных условиях более низкую скорость сваливания на крыло, что для учебки очень важно. Однако, тренировать на нем навыки выполнения фигур пилотажа неудобно, поскольку он имеет ярко выраженную асимметрию характеристик. У тренировочной модели должен быть тот же профиль и та же нагрузка на крыло, что и у пилотажки, на которой пилот будет выступать на соревнованиях.
Бесхвостка
Помимо самолетов обычной схемы с оперением, бывают самолеты без оперения. Чаще всего киль все-таки сохраняется в том или ином виде, а вот стабилизатора нет вовсе. О достоинствах и недостатках такой аэродинамической схемы мы говорить здесь не будем. Балансировка и продольная устойчивость таких самолетов достигается за счет различных конструктивных ухищрений. Но, если крыло бесхвостки не стреловидное, а прямое, то единственный способ обеспечить балансировку и продольную устойчивость самолета – применить на крыле самобалансирующийся профиль:
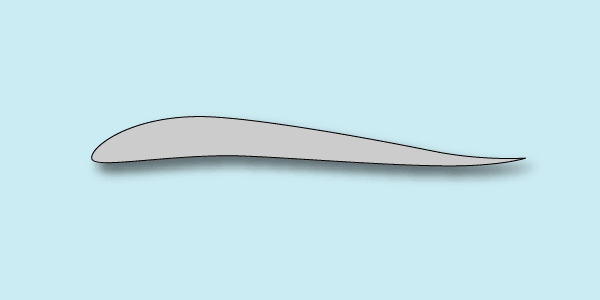
Как видно, у таких профилей кривизна меняет вдоль хорды свой знак. В передней части профиля он выпуклый вверх, в задней – вниз. Такие профили еще называют S-образными, потому что средняя линия профиля напоминает латинскую букву S. Чем замечательны эти профили? У обычного несимметричного профиля при увеличении угла атаки точка приложения аэродинамической силы R смещается по хорде профиля вперед. При этом момент крыла, способствующий подъему носа самолета, увеличивается с ростом угла атаки. Крыло с таким профилем само по себе, без оперения устойчивым быть не может. У S-профилей наоборот. В диапазоне летных углов атаки увеличение этого угла приводит к смещению точки приложения аэродинамической силы по хорде профиля назад. В результате появляется момент на пикирование, стремящийся вернуть угол атаки к первоначальному значению.
К сожалению, в жизни не бывает, чтобы к бочке меда не добавили ложку дегтя. Так и здесь. Увесистая ложка дегтя: у S-профилей значительно более низкие предельные значения Су. Это заставляет конструктора самолета при равной с обычной аэродинамической схемой скорости полета делать у бесхвостки гораздо меньшую нагрузку на крыло, то есть значительно увеличивать площадь крыла при равном весе с самолетом обычной схемы.
Копия
Модели-копии в силу своего предназначения должны копировать все геометрические формы оригинала. В том числе и профиль крыла, иначе какая же это копия. Однако, число Re у копий намного ниже, чем у оригинала. Как будет летать такая модель?
При масштабном уменьшении и снижении чисел Re аэродинамическое качество снижается. Безмоторные копии летают хуже своих оригиналов. Для моделей вязкость воздуха играет гораздо большую роль. Однако, снижение летных свойств вовсе не катастрофично. От копий, как правило, и не требуется выдающихся аэродинамических характеристик. К тому же моторные модели, как правило, имеют большую энерговооруженность, чем копируемые оригиналы. В результате чего их летные свойства при точном копировании профиля крыла вполне удовлетворительны. Есть даже примеры обратной зависимости. На бипланах времен первой мировой войны широко использовались тонкие сильно изогнутые профили крыльев. Вовсе не потому, что они оптимальны для полетных чисел Re, а по конструктивно-технологическим причинам – их проще было делать для расчалочных крыльев деревянно-полотняной конструкции. При переходе к уменьшенным копиям, такой профиль оказывается более оптимален, чем у оригинала.
Для моделей современных сверхзвуковых самолетов приходится отступать от копийности профиля крыла, поскольку очень тонкие профили оригиналов с острым носиком определяют крайне неудовлетворительные срывные свойства у копий. Приходится мириться с неполной копийностью.
Радиопланер
Как было указано выше, оптимален тот или иной профиль крыла только при вполне определенных числах Re. Чем шире у модели диапазон полетных скоростей, тем труднее оптимизировать профиль ее крыла. Из всех видов крылатых моделей, один из самых больших диапазонов полетных скоростей у кроссовых радиопланеров F3B. В упражнении на продолжительность этому планеру выгодно лететь как можно медленнее, особенно в атермичную погоду. Скорость полета не превышает 7 – 8 м/сек. В упражнении на скорость планера разгоняются до скоростей в 40 – 45 м/сек. Для расширения диапазона чисел Re широко используют механизацию крыла. На кроссовых планерах вдоль всей задней кромки крыла размещена механизация, – на корневой половине консолей – закрылки, на концевой – элероны, смикшированные, как правило, с закрылками. В результате пилот имеет возможность в полете менять эффективную кривизну профиля крыла при помощи механизации, оптимизируя ее под требуемый режим полета. Используется как правило три, реже четыре режима предустановленные в процессе регулировки и переключаемые в полете пилотом. В стартовом режиме кривизна максимальна. Это делается для увеличения максимально возможного значения Су, которое определяет скорость затяжки на леере планера относительно буксировщика леера. В конечном итоге это определяет высоту старта при ограниченной правилами длине леера. Сх при этом значителен, а аэродинамическое качество невелико. Но это и не важно, поскольку энергия поступает извне – от буксировщика. Крутые пилоты используют при старте два предустановленных режима – в начале и в конце с разной кривизной профиля. На режиме парения механизация возвращает кривизну профиля к исходной, где его аэродинамическое качество максимально. Для скоростных режимов механизация слегка приподнимает заднюю кромку крыла, создавая минимальную эквивалентную кривизну профиля. Сх принимает свое наименьшее значение.
Сейчас наиболее распространены для кроссовых планеров профили серий MH, RG и HQ. Их разработчики при оптимизации геометрии профиля учитывают поведение аэродинамических характеристик при работе механизации крыла. Для справки можно привести профили 16 типов моделей финалистов чемпионата Мира по F3B 2001 года. На шести моделях стоял профиль MH-32, по две модели использовали профили HQW-3.0, RG-15 и SD7037. На остальных моделях, не занявших призовых мест, использовались оригинальные профили. Но на чемпионате Европы 2004 года MH-32 лишь у одного из спортсменов первой десятки. Призовые же места у SD7032 и RG-15.
Упрощенные профили
В некоторых случаях, чаще всего из конструктивных соображений, упрощают контуры профиля до примитива, когда его образующие – прямые линии. Иногда – они оправданы, в других случаях – нет. Для наглядности приведем по одному примеру таких случаев.
В последние пару лет появился новый класс авиамоделей – F3AI ( I здесь от Indoor – внутрикомнатный ) пилотаж внутри помещений. Самолеты этого класса имеют очень маленькую нагрузку на крыло и летают ни крайне низких числах Рейнольдса. Многие из них имеют крыло в виде тонкой прямой пластины из депрона с угольными передней и задней кромками. Такой профиль имеет малое значение максимального Су. Однако для крайне малых нагрузок на крыло это не важно. Срывные характеристики профиля тоже ужасны. Полет самолета больше напоминает порхание стрекозы, чем полет аиста. Тем не менее, такие самолеты показывают 3Dпилотаж весьма высокого уровня. Это – пример оправданного упрощения.
Некоторые начинающие в стремлении упростить изготовление крыла тренировочной модели сводят его профиль к примитивному треугольнику, где две вершины – острые передняя и задняя кромки, а третья – верхняя полка лонжерона. Нижняя полка лежит на плоской нижней поверхности крыла. Что может быть проще? Однако летать на таком крыле – неинтересно. Прошедшим летом, наблюдая за мучениями такого горе-конструктора, жалко становилось не его, а самолет, - на пять взлетов – две посадки. Остальные посадки – «кирпичом». К концу полетного дня от модели, и кстати – мотора, остались жалкие дрова. Такой профиль имеет низкое значение Су на предельных углах атаки и провоцирует к тому же лавинообразный срыв потока. Модель просто летит кубарем к земле. Это - пример неоправданного упрощения.
Резюме
Поскольку разнообразие видов крылатых моделей очень велико, мы не будем детально рассматривать особенности применяемых в них профилей крыла. Подведем итог в виде описания характера влияния геометрических параметров профиля на его аэродинамические свойства. Итак:
- Толщина профиля – влияет на величину лобового сопротивления. Увеличение толщины увеличивает сопротивление, в том числе на нулевой подъемной силе. Косвенно, увеличение толщины приводит к срыву обтекания на больших углах атаки, чем у тонких профилей. Увеличение толщины от малых значений до 12 – 15% увеличивает максимальное значение Су. Дальнейшее увеличение толщины его снижает. После 20% резко растет Сх.
- Радиус скругления носика профиля – связан с толщиной профиля. Влияет в первую очередь на поведение профиля на критических углах атаки. Косвенно влияет на лобовое сопротивление профиля. Большие значения радиуса приемлемы только на невысоких числах Re.
- Кривизна профиля – влияет на асимметрию свойств. Увеличение кривизны приводит к увеличению Су на сравнительно небольших числах Re. При росте Re кривизна профиля для сохранения приемлемых значений лобового сопротивления должна уменьшаться.
- Для обеспечения высокой эффективности профиля в большом диапазоне скоростей на крыле необходимо использовать механизацию, изменяющую в полете эффективную кривизну профиля для разных скоростей.
- Свойства профиля крыла влияют на требуемую для балансировки и продольной устойчивости самолета эффективность горизонтального оперения, что необходимо учитывать при проектировании модели в целом.
Характеристики несущего крыла зависят не только от примененного профиля, но и от ряда других его геометрических параметров. Их определение и характер влияния на аэродинамику крыла будет рассмотрен во второй части статьи.
Обсудить на форуме